最高のコレクション 直方体 の 求め 方 324953

J = ρ∫ b −b( 2 3a3 2ay2)dy J = ρ ∫ − b b ( 2 3 a 3 2 a y 2) d y J = ρ( 4 3a3b 4 3ab3) J = ρ ( 4 3 a 3 b 4 3 a b 3) J = 1 3 m(a2 b2) J = 1 3 m ( a 2 b 2) となります。 ここで直方体の慣性モーメントですが、長方形の慣性モーメントを z z 軸方向に積み重ねていけば、直方体の慣性モーメントになります。 これは円柱の慣性モーメントの章で説明したように、直方体の高さによらず一定に無料授業動画サイト「StudyDoctor」 http//studydoctorjp/家庭教師テキスト http//studydoctorjp/?page_id=4英語はmiki先生 https//www立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習

動画で学習 2 いろいろな体積の単位 算数

直方体 の 求め 方

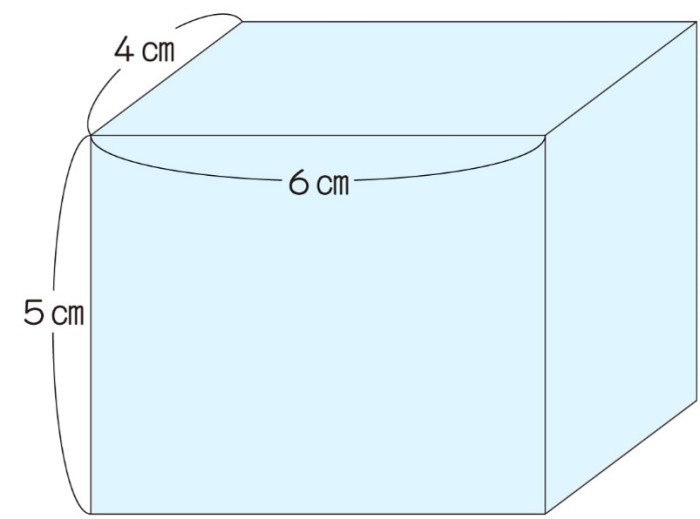
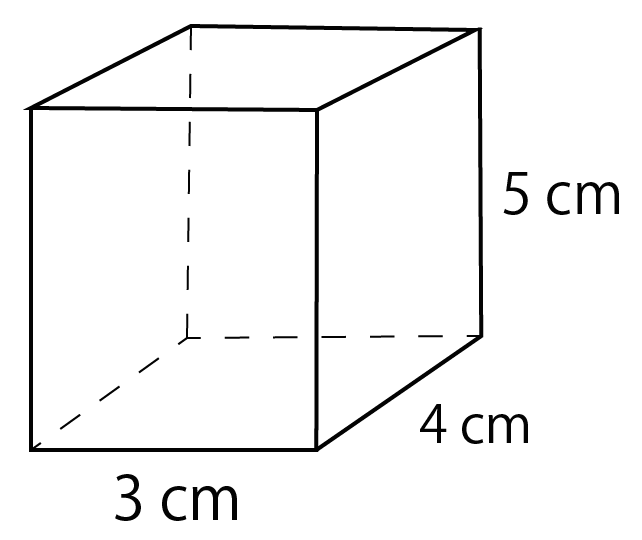
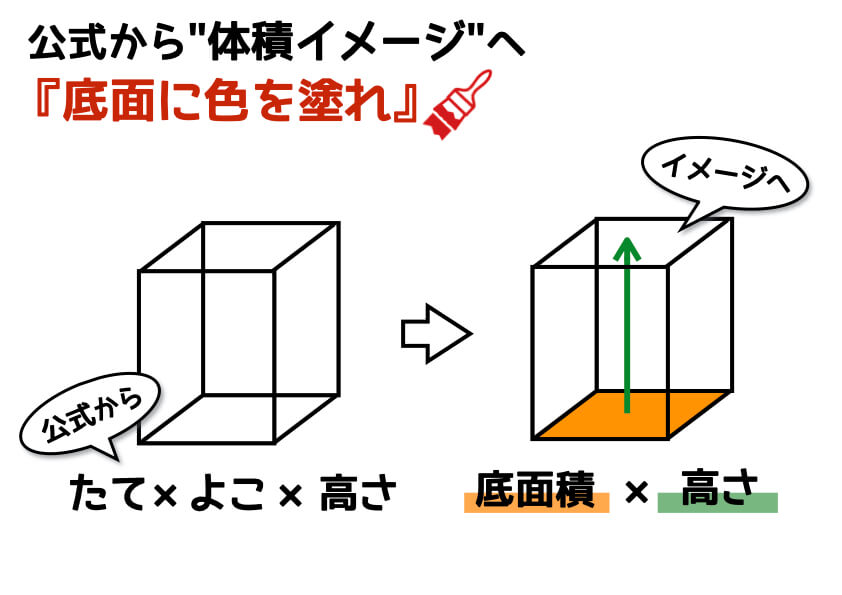
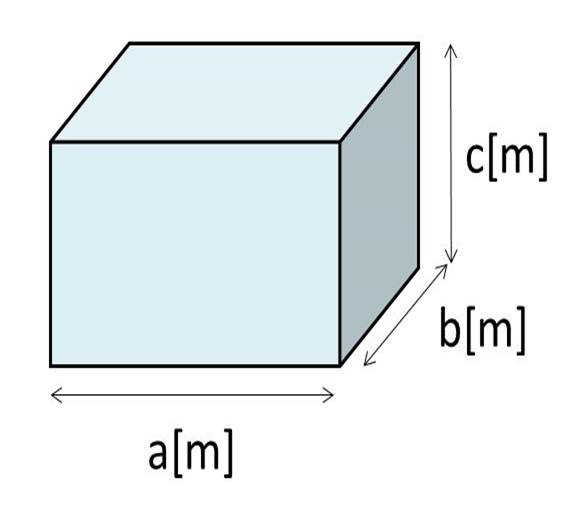
直方体 の 求め 方-直方体や立方体の体積の公式 直方体の体積 ＝（ ）×（ ）×（ ） 立方体の体積 ＝ ×（ ×（ ） 公式を使って直方体と立方体の体積を求めよう。 たて 横 高さ 1辺 1辺 1辺 6 7 5 210 210 8 8 8 512 512> ・簡単な式であらわされている二つの数量の関係を調べる > > >（小6から移行） ・体積の単位（㎤、㎥）と測定 ・立方体 直方体の体積の求め方 >

立方体の対角線の長さの求め方

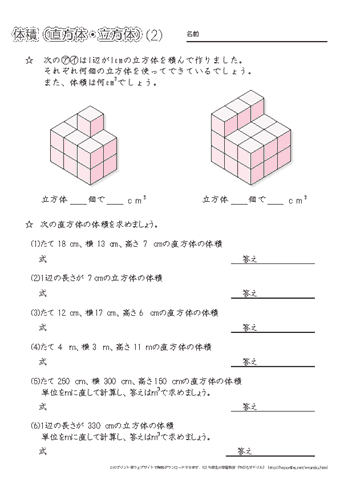
直方体の容積を，リットル単位で求める方法を教えて 無断複製・転載・翻訳を禁ず gakken b (容積の文章題) 中学理科3分でわかる！密度の求め方・出し方の計算公式 中学理科で密度の求め方・出し方の公式がわからない！ こんにちは！この記事を書いてるKenだよ。タンパク質最高。 中学理科の「身のまわりの物質」という単元では、 密度の求め方直方体と立方体の体積の求め方を考えます。 1辺が 1 cm の立方体が何個分あるかで求めることができます。 縦×横×高さ＝直方体の体積，1辺×1辺×1辺＝立方体の体積となります。

答え 体積の求め方を考えよう。 1辺 1辺 1辺 横 高さ たて ①直方体の体積は，どのような式で 表すことができますか。 ②立方体の体積は，どのような式で 表すことができますか。 直方体の体積＝たて×横×高 さ 立方体の体積＝1辺×1辺×1辺 次へ直方体を組み合わせた立体の体積の求め方を,求積できる形に変形して,説明することができる。 思考・判断・表現 （2）評価規準 既習の直方体や立方体の形を基に,直方体を組み合わせた立体の体積の求め方を図や式を用いて考 え,説明している。中学数学（三平方の定理）：直方体の表面上の最短距離 1． 三平方の定理とは 2． 直角二等辺三角形 4． 証明（図形的に） 5． 直方体の対角線

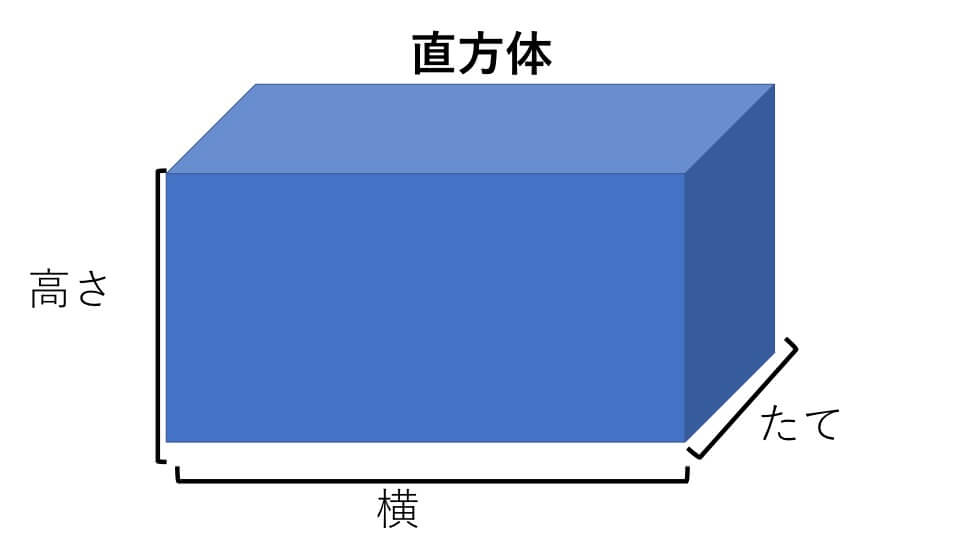
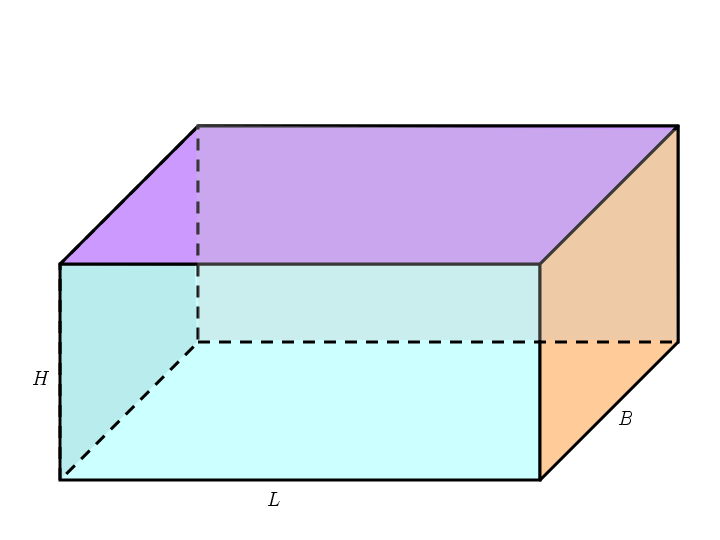
長方形が積み上がってできた 6 6 つの面からなる立体図形を 『直方体』 と言い、すべての辺の長さが同じで 6 6 面がすべて正方形からなる直方体を 『立方体』 と言います。 直方体の体積は『縦×横』の長方形が『高さ』分だけ積み上がったと考えると、体積は 『縦×横×高さ』 です。 立方体の場合、縦・横・高さがすべて一辺の長さとなるので、体積は 『1辺×1辺×1直方体の縦・横・高さを入力 縦 = 2 横 = 4 高さ = 5 直方体の体積 v = 直方体の表面積 s = 直方体の縦・横・高さを入力 縦 = 34 横 = 52 高さ = 41 直方体の体積 v = 724 直方体の表面積 s = 1050 このように入力した縦・横・高さに対する体積と表  立方体や直方体の体積の求め方を習ったら、少し応用的な問題にも取り組みましょう。展開図を見て、体積を求める問題や、いくつかの立方体や直方体の面積を足したり引いたりして解く問題です。 直方体の体積を求め

くふうして体積を計算しよう 家庭学習レシピ

小5算数 直方体や立方体の体積の意味と単位がわかるかな Youtube

ぼくは，直方体の一部が欠けた形とみて，大きな直方体の体積から 欠けている部分の直方体の体積をひいて求めました。 ひとし わたしは，この形を2つ組み合わせると1つの直方体になると考え， その直方体の体積の半分を求めました。 めぐみ ㋐ 3×2×3÷2直方体の慣性モーメントの計算過程。 x軸y軸z軸まわりにおけるそれぞれの慣性モーメントを、微小体積要素を求め、さらには微小体積要素部分の慣性モーメントdIをたし上げることにより慣性モーメントを導き出します。 使用する座標系はデカルト座標系を用います。 慣性モーメント計算 > 直方体の慣性モーメント 直方体の慣性モーメント トップページ直方体の体積から，高さを求めるには，どうするの 無断複製・転載・翻訳を禁ず gakken b

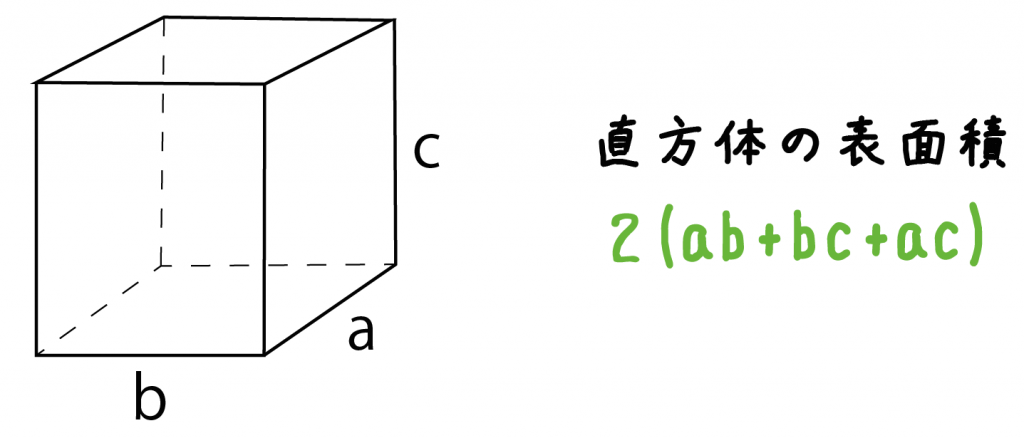
表面積の求め方 計算公式一覧

水の中に立体を入れる問題の解き方 お風呂に入るとお湯があふれるあの現象

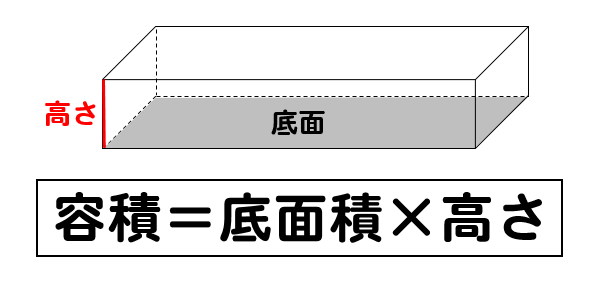
⑤ まとめて，角柱の体積は，底面積×高さの式で求められる。 この考え方は第5学年で学習した直方体の体積の求め方が基盤となっており，これを基に， 未習である角柱の体積の求め方を考え，解決していくことができる。このことを，児童自身・直方体や立方体の体積を，公式を使っ て求める。 5 本 時 で直方体を組み 既習事項を活用 して，多様な方法 合わせた図形の 体積の求め方を 考え，求めること ができる。 ・直方体を組み合わせた図形の体積の求 め方を工夫しながら多様に考える。数学・算数 直方体の体積の求め方は横×縦×高さでは間違い？ 小学5年生の算数のテストで、直方体の面積を求める問題がありました。 公式は縦×横×高さとなっていますが、横×縦×高さの順で式を書きました 質問No

計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

４年算数 直方体と立方体 １ わかる教え方のポイント

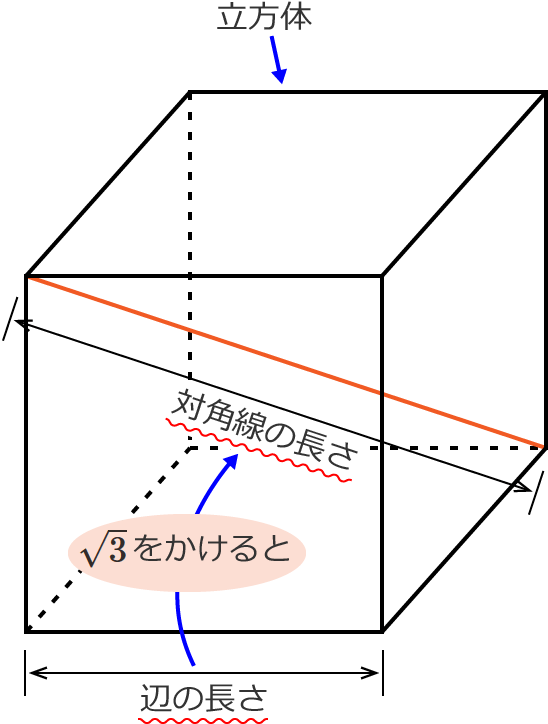
慣性モーメントの導出：直方体 21年1月12日 下の図のような質量m、それぞれの辺の長さがa , b , lの直方体の慣性モーメントを求めます 密度をρとすると ρ = m a b l 積分範囲は − b 2 ≤ x ≤ b 2 − a 2 ≤ y ≤ a 2 − c 2 ≤ z ≤ c 2 z軸まわりの慣性モーメントまとめ！ お疲れ様でした！ 直方体や立方体の対角線の長さは、 2つの直角三角形に注目することで求めることができます。 ですが、公式を覚えておけば 計算の手間をかなり省けるのでおススメです！ なので、公式をしっかりと使いこなせるようにして年 組 番 名前 524 直方体や立方体の体積 体積の求め方の工夫 下のような形の体積を求めます。 かのんの考え方で、体積を計算して求めましょう。

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

体積の測定 測定のことを 即 知りたい ソクシリ キーエンス

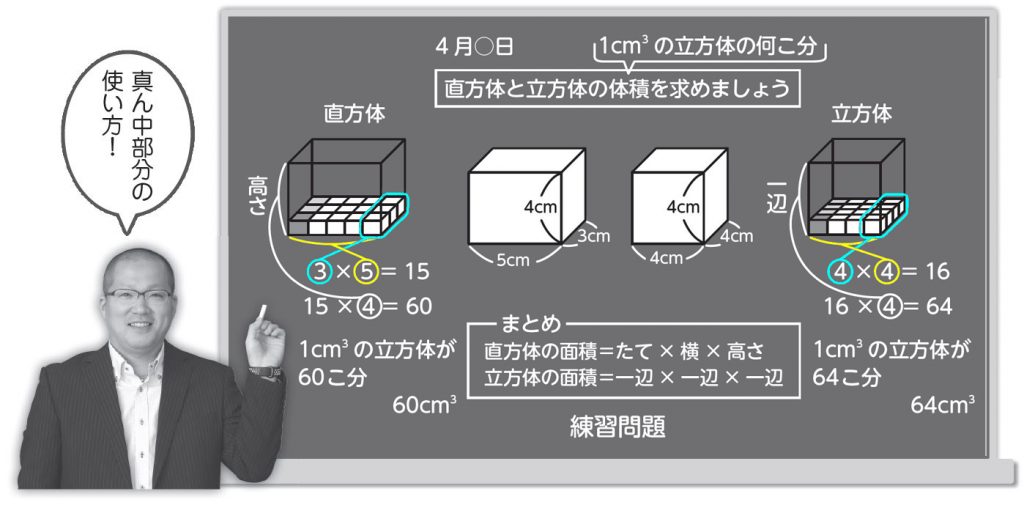
めあて「直方体や立方体の体積を、計筤で求める方法を考えよう。」 (2) ノートに＜問題＞を書きましょう。㋒と㋓の図もかいてみよう！ ＜問題＞㋒の直方体と㋓の立方体の体積を求めましょう。 (3) p19①㋒の直方体は、1 ㎤ の立方体の何こ分か調べ②直方体と立方体の体積の公式と使い方 ③容積の意味と求め方 ④複合図形の体積の求め方 教え方1 直方体のかさの大きさくらべを通して、かさの大きさを1 の単位で表す方法を教えます。 問題 下の図の二つの直方体の大きさをくらべましょう。立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積（底辺と高さから） 正四角錐の体積（底辺と側辺から）

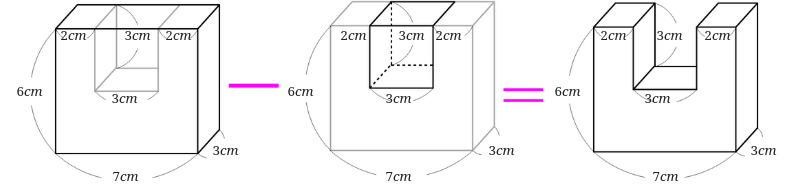
直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校

面積や体積の概念 奈良市立都祁小学校

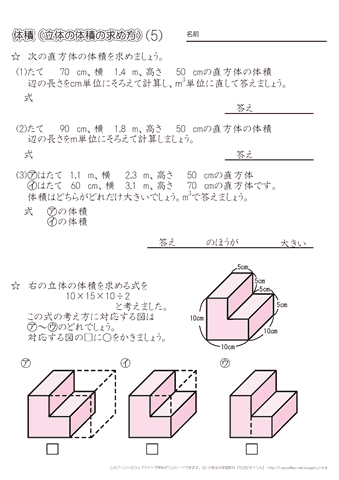
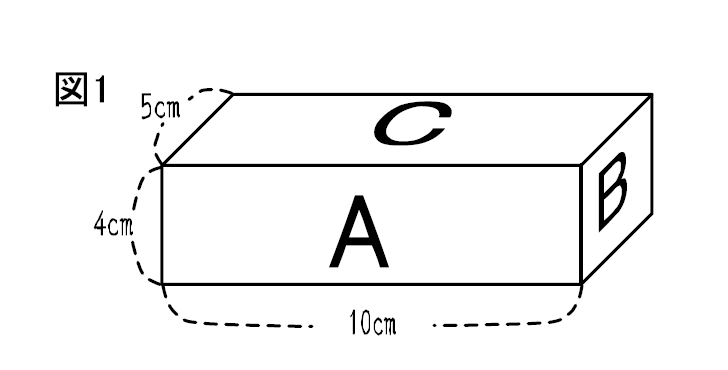
次に，点線で囲んでいる小さな直方体（C）の体積を求めます。たてが12－8，横が15－10で 全体の体積から 点線で囲んでいる小さな体積を引くと，7－80＝640となり，この体積が 求められます。 1mは100cmなので，1m3 立方体，直方体の体積は，辺の長さが小数で直方体の体積は「縦×横×高さ」で求めます。よって、 となります。 まとめ 今回は直方体の表面積の求め方について説明しました。直方体の表面積Sは、S=2ab2bc2acで計算します。直方体は6面の長方形で構成される立体図形です。また、向かい合う面は同じ形状なので、3面の面積を合計した値を2倍すれば直方体の面積が算定できます。直方体や立方体のかさの表し方を考えよう ㋒の直方体と㋓の立方体の体積を求めましょう。 ㋒の立方体は、1㎤の立方体の何個分か調べましょう。 （1）1だんめには、1㎤の立方体が何こならびますか。 （2）何だん積めますか。

物体の重心

1

れらの求め方を考え、求 めようとしている。 既習の学習事項を基 に、辺の長さを用いた計 算によって体積が求め られることを考えてい る。 公式を用いて体積を 求めることができる。 単位と測定の意味や、 直方体や立方体の体積 の求め方を理解し、体積 圧力を計算できる公式は、 圧力 Pa = 面を垂直におす力 N ÷ 力がはたらく面積 m²そして，立体をゆっくり回転させ，次第にL字型であることを理解させる。初めに見せる形から既習の立方体や直方体の体積の求め方を確認させるだけではなく，複雑な形の体積の求め方という本時の課題をはっきりさせる。 → → →

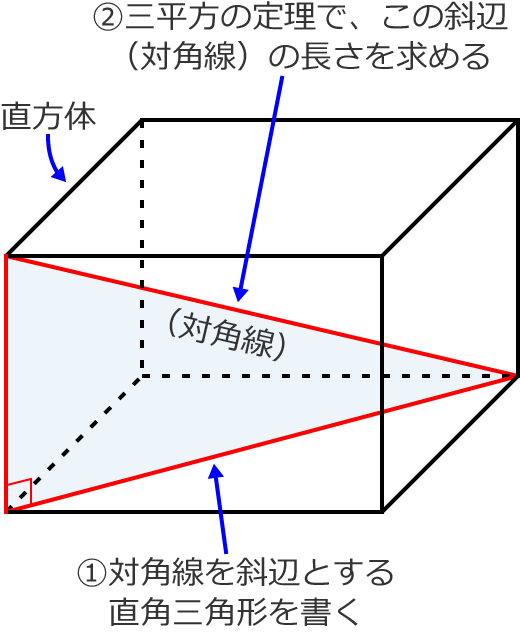
直方体の対角線の長さの求め方

立体の体積は平行線でね 基本に忠実に本質を伝える 楽天ブログ

直方体の置き方を変えると、式が変わります。 教科書どおりの立式です。 そして、どう置くかは、個人の自由ではないでしょうか？ 置き方を変えても、体積が変わるわけはありません。 これが、ビルの体積を求めなさいという問題なら話は別ですが、手がかりは辺の長さだけ！ 今回は、 「直方体の切り口の面積」 を求める問題を扱うよ。 下の図を見てみよう。 こんな風に、直方体をスパっと切るわけだね。 そこで 切り口の三角形の面積 を求めようという問題だよ。 分かっている情報は 直方体の辺の長さ だけなんだ。 そこから 切り口の面積 を求めるとなると、かなり話に飛躍があるよね。 この飛躍したP19～ も ウの直方体と エの立方体の体積を求めましょう。 か 直方体や立方体の体積を計算で求める方法を考えよう。 1㎤の立方体が何こあるのかを求めるには？ ・面積の時には計算で求めたから・・・。 ・求め方をかけ算の式で表したから・・・。

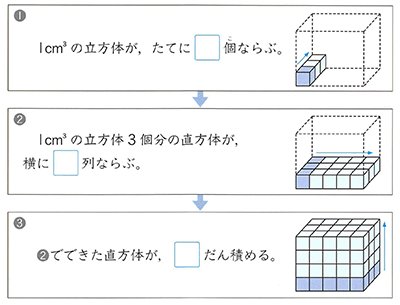
Kistenkasten723 ５年生は どうして 直方体の体積が縦 奥行 横 幅 高さという公式で求められるかを学習しています 単元テストは 入試や検定試験などと違い 授業の一環であり 授業でやったことができるかどうかを確認するのが目的です

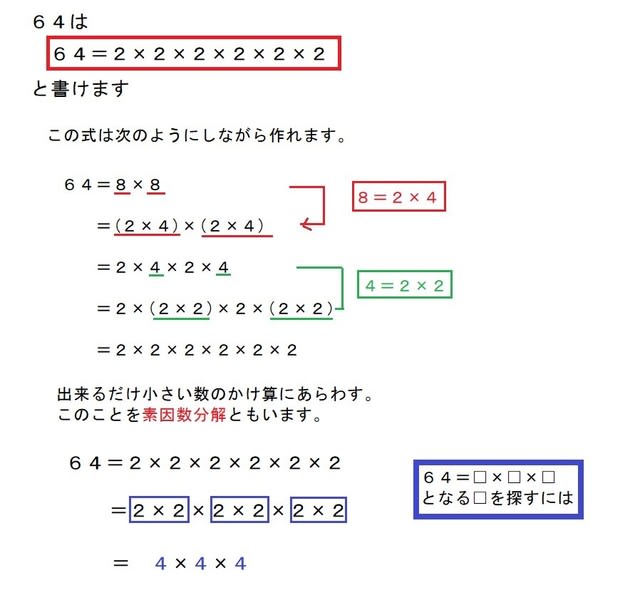
直方体 立方体の体積 小５ きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support

計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

二次方程式の利用 箱の容積を考える文章問題を解説 数スタ

体積の求め方 計算公式一覧

体積の求め方 計算公式一覧

最高かつ最も包括的な直方体 の 表面積 の 求め 方 最高のぬりえ

動画で学習 2 いろいろな体積の単位 算数

直方体 Wikipedia

H21面積

角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題

立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 数学ノート

兵庫県実践事例 算数小学校６年

立方体の対角線の長さの求め方

中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット

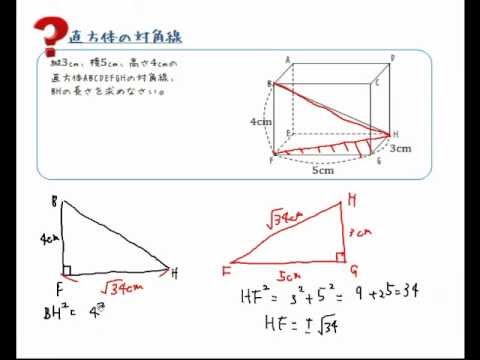
三平方の定理 直方体の対角線を求める Youtube

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

2

Http Www Dainippon Tosho Co Jp Newsletter Files Es Math Test26 Pdf

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強

算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ

計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

小学校５年 算数 直方体や立方体のかさの表し方を考えよう シンキングツール 思考ツール 授業案

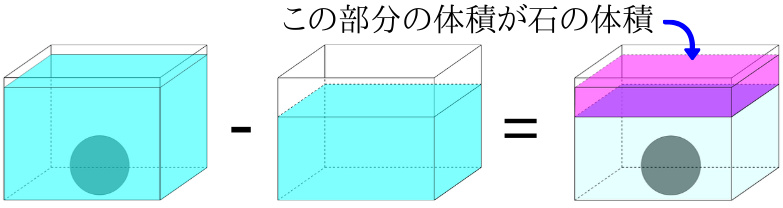
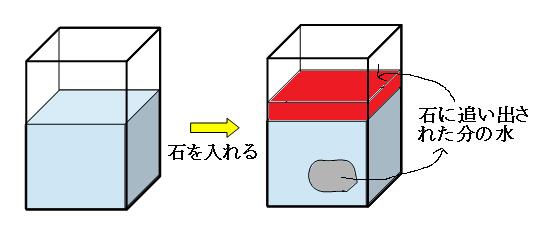
石を水の入った水槽に沈めて体積を求める問題の教え方 みけねこ小学校

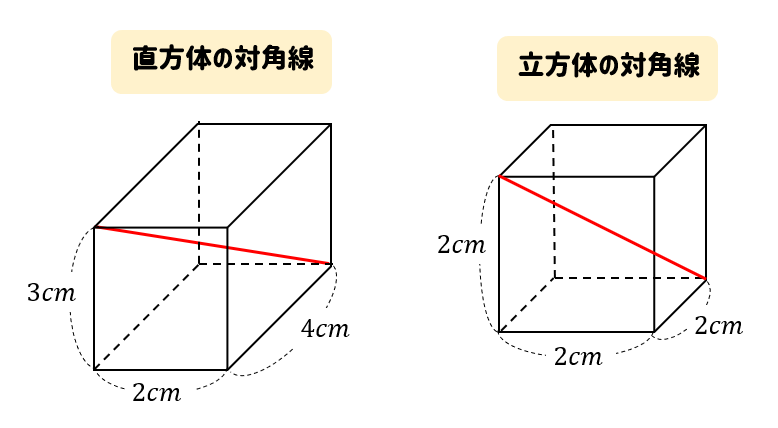
直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ

75 5 年生 体積とは 最高のぬりえ

直方体の表面積の求め方 Youtube

直方体の慣性モーメントの求め方について質問があります 下図 Yahoo 知恵袋

D 1 2 4cm 3cm 4c 5cm Ic Descubre Como Resolverlo En Qanda

６年算数立体の体積１ 教え方

小学５年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生

立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun

25 Descubre Como Resolverlo En Qanda

3times 7 4 Times 2 1 Descubre Como Resolverlo En Qanda

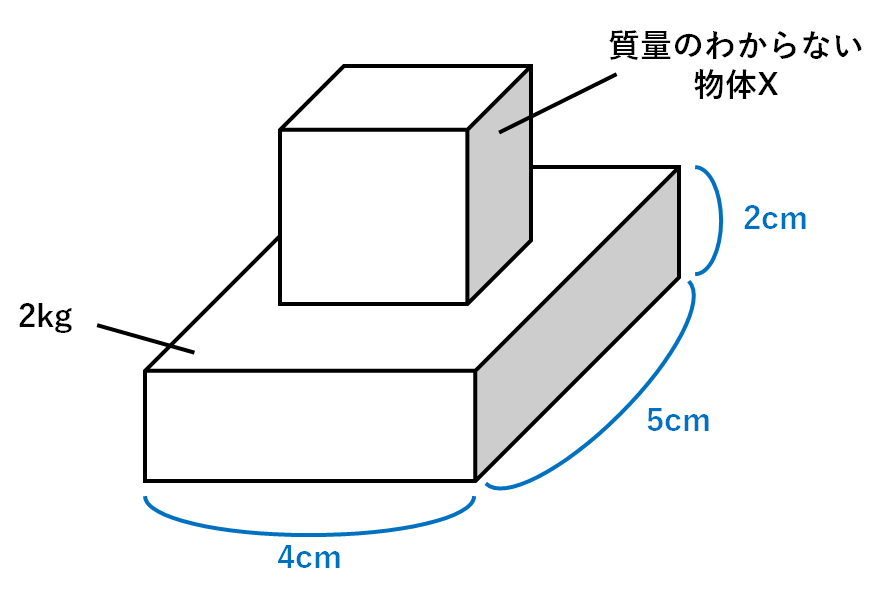
中2地学 圧力 中学理科 ポイントまとめと整理

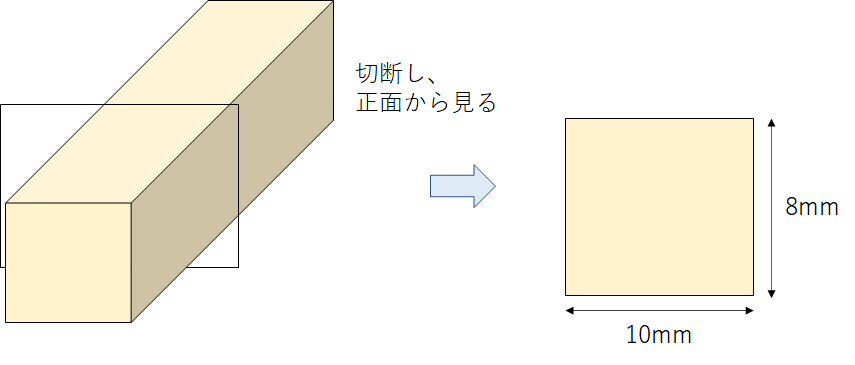
9vgfusfl6xfevm

面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張

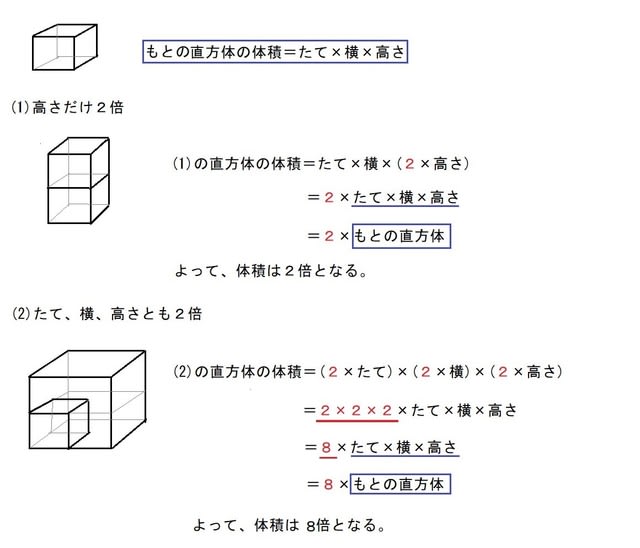
直方体 立方体の体積 小５ きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

多くの教師が失敗する角柱の体積の求め方 算数を究める

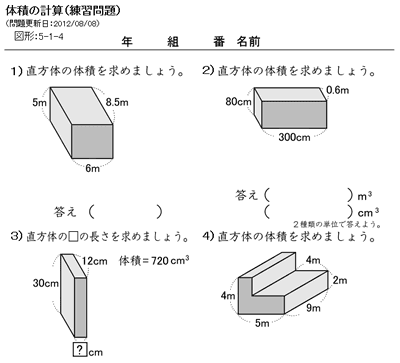
最高かつ最も包括的な5年生 算数 体積 プリント 最高のぬりえ

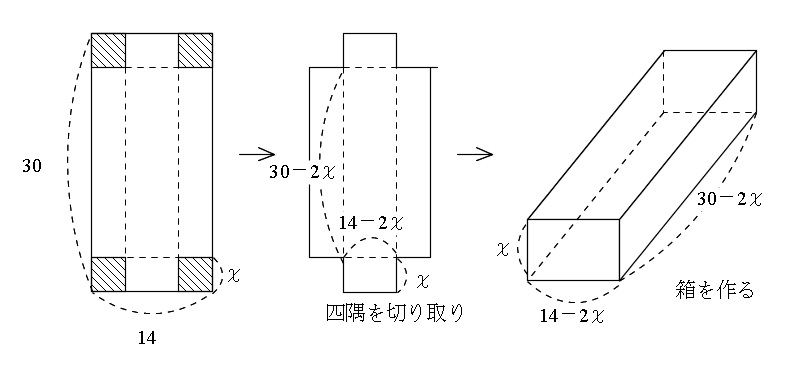
微分を使って直方体の容積の最大値を求める方法

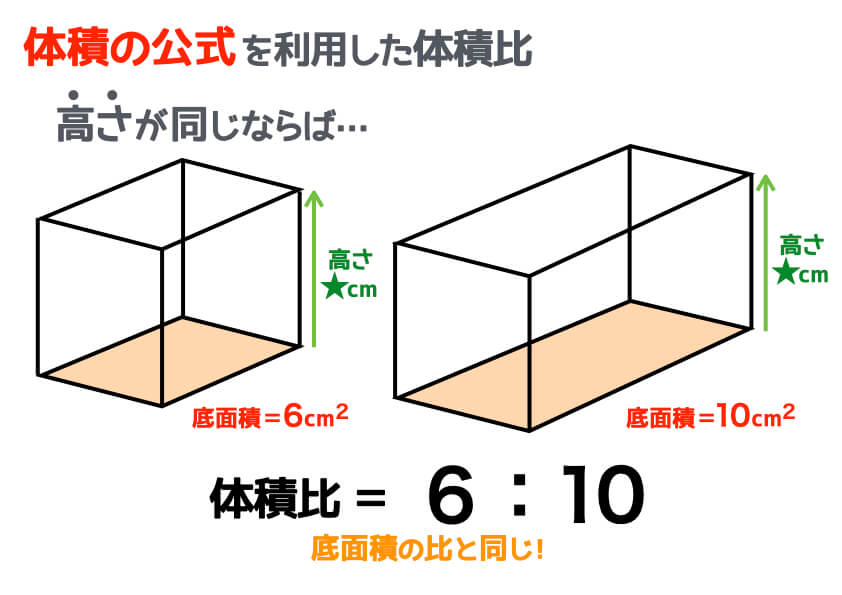
小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ

小5算数 直方体や立方体の体積の求め方がわかるかな Youtube

Www Saga Ed Jp Kenkyu Kenkyu Chousa R2 01 Syo Chu Kakukyouka 02 Syo Sansu 1 Pdf 5nen R2 5 1 2 Taiseki Pdf

面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

トライなどがネットで無料授業 サービス増加 予習に活用 確認テストも 産経ニュース

計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

1

公式を図解 すい体の体積 円すいの表面積の求め方

小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ

マスラボ 小学５年 直方体や立方体の体積 体積の求め方の工夫 Youtube

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

5年 直方体と立方体の体積 算数イメージ動画集 大日本図書

小学５年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生

パワーポイント教材 那須烏山市立烏山小学校

Excel エクセルで立方体 直方体の体積の計算を行う方法 立方メートル モッカイ

体積 直方体 立方体 ５ 算数 算数 問題 算術

1

Studydoctor直方体の対角線の長さの求め方 中学３年数学 Studydoctor

小学5年生の算数 動画 直方体と立方体の体積 の問題 19ch

直方体 の 体積 の 求め 方 公式

斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル

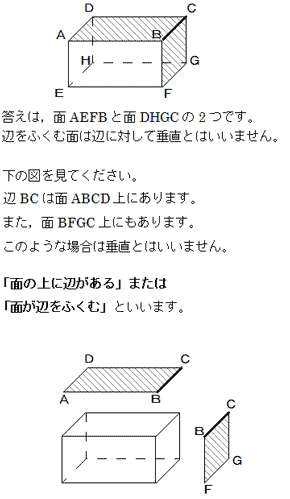
空間図形 辺に垂直な面がどこか という問題 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ

体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座

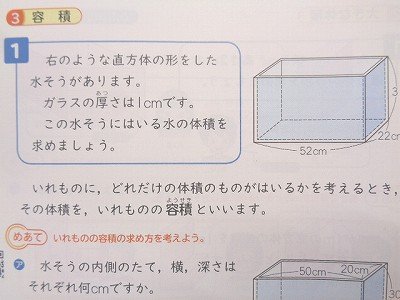
4 30木 算数科 理科通信 造形室からこんにちは 京都文教短期大学付属小学校

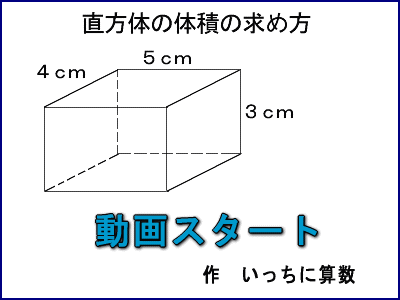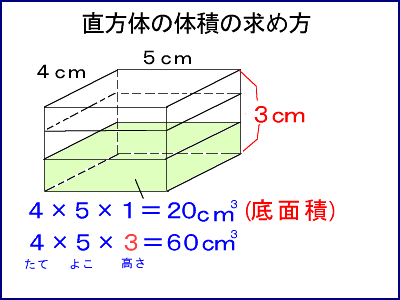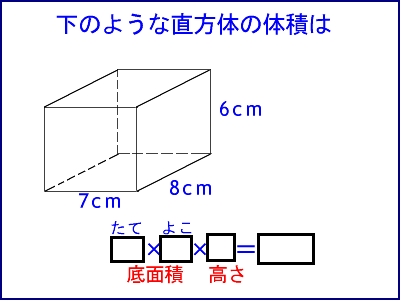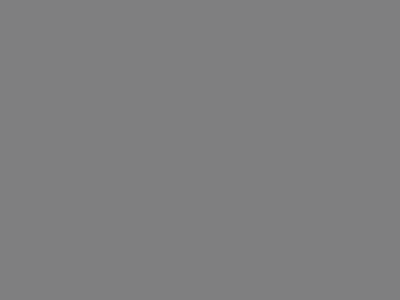
６年算数立体の体積１ 教え方

超簡単 体積の求め方 苦手な数学を簡単に

直方体の体積は 縦 横 高さ じゃなくても求められる ジョン曰く

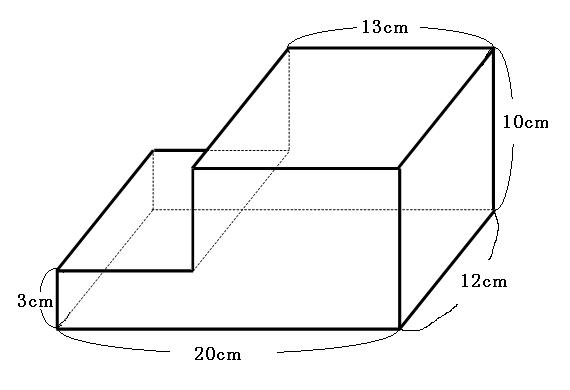
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか

公式を図解 すい体の体積 円すいの表面積の求め方

小学算数 構造的板書 の工夫とコツ 小数 体積 みんなの教育技術

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

体積の求め方 計算公式一覧

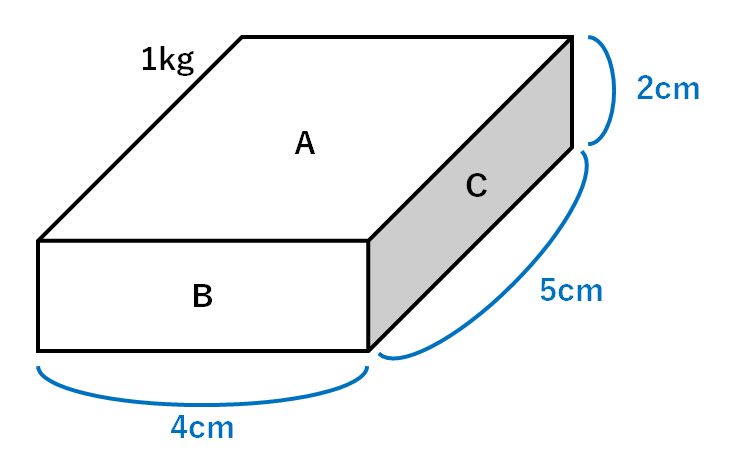
中2地学 圧力 中学理科 ポイントまとめと整理

空間図形です 写真の図のaiの長さの求め方を解説お願いします また 各辺の長さは写真 Clear

積分定数 超算数 T Co 2hispbds9u 真面目で良心的な教員志望の人の発言だが それでも超算数の悪影響を受けている 立方体 直方体の面積の求め方は 縦 横 高さだけど 横 高さ 縦でもその他でもいい なお 超算数的には 立方体は縦 横 高さ

1

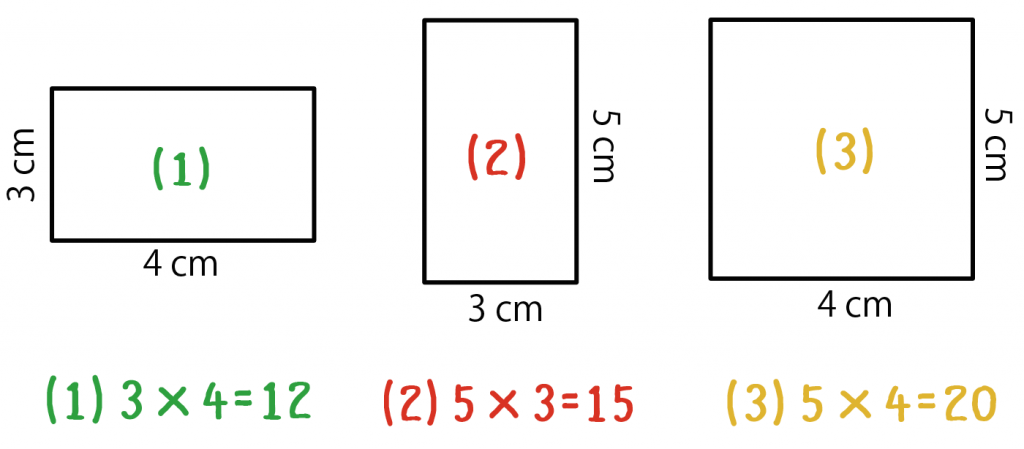
計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

圧力の計算

ページタイトル

直方体や立方体のかさの表し方を考えよう 国際算数数学授業研究プロジェクト Impuls International Math Teacher Professionalization Using Lesson Study

毎日問題を解こう 18 苦手な数学を簡単に

前も似たような動画の解説でわからなかったんですがなぜ A Clear

体積のドリル

12 3cm 5cm Descubre Como Resolverlo En Qanda

体積 上 体積の意味から 立方体 直方体 柱 錐の体積の求め方 思考力算数練習張シリーズ 46 エム アクセス 本 通販 Amazon

計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun